How do Molecules Behave?

• On molecular level, so-called deterministic chaos can be observed. Any minute perturbation of a molecule leads to divergent behavior of that molecule, which is a so-called Lyapunov instability. As a consequence, it is practically impossible to predict the behavior of a system with sufficient accuracy over some intermediate time interval, because the starting conditions of the system would need to be defined with an accuracy, which quickly increases as the prediction time is increased.

• If the interactions between particles are included in the considerations, the situation gets considerably worse. It turns out that interactions even from the farthest particles will influence the behavior of an observed particle after at most 33ps (33 times a millionth of a millionth of a second). The effect is complete randomization after at most that short time. Also, the horizon that needs to be accounted for includes all particles within the observable universe and their behavior since the big bang. Thus, there exists a highly interlinked and quickly reacting network of interactions between all particles in the universe. On molecular level the behavior can thus only be regarded as unpredictable and random.

• As a secondary consideration, the direction of time can be regarded. While most physical laws are invariant to the inversion of the direction of time, the initial conditions are not. In forward direction of time, the initial conditions can be chosen arbitrarily. In backward direction of time, as soon as more than 33ps shall be observed, they would need to fulfill the condition that all interactions develop backward in time properly and consistently until the big bang. The direction of time thus does not relate to the physical laws themselves but the definition of the initial conditions. The question on the direction of time of course only relates to our description of reality and not necessarily to reality itself.
  

• These considerations assume a fully deterministic world view, which means that with the exact physical laws, a given starting situation will lead to an unavoidable and unique future development, which is solely defined by the physical laws and the initial conditions.

The discussion presented here has largely been previously published as:
Pfennig, A.: On the strong influence of molecular interactions over large distances.
Eur. Phys. J. D (2018) 72: 45. https://doi.org/10.1140/epjd/e2017-80293-4.

By evaluating the behavior of molecules as simulated on a computer, it turns out that on molecular level so-called deterministic chaos can be observed. This is defined such that any small perturbation of one of the molecules will lead to an exponentially increasing deviation of the position of that molecule as compared to the case, where the perturbation has not been introduced. To quantify this exponentially increasing behavior, simulations tracing the path of molecules by evaluating the forces acting between them and then solving Newton's equation of motion have been performed for liquid water at 37°C. One simulation has been performed without a perturbation, in a second simulation a small shift in position of a single water molecule was introduced, and the following path of that molecule recorded. Comparing the pathways of molecules of both simulations, their so-called trajectories, the continual increase in deviation of the positions of the observed molecule can be obtained as shown in Figure 1. It is obvious from the logarithmic scaling of the vertical axis and the then almost linear behavior as function of time, that indeed an exponential increase of deviation in position is observed. The two compared simulations diverge exponentially. By comparing the behavior for different starting perturbations as well as for varied simulation parameters like step width of integration and system size, it can be shown that this behavior is characteristic for the system as such and not just induced by the specific simulation algorithm used. This divergence establishes the determinstic chaos and corresponds to a so-called Lyapunov instability. Quantitative evaluation shows that the deviation in position increases by a factor of 10 every 0.23ps (ps = pico second = the millionth part of the millionth part of a second). This effect is called deterministic chaos, because all equations describing the system behavior are exactly defined and in principle allow to predict molecular behavior. If the starting conditions would be exactly defined, the system behavior would be exactly determined into an arbitrarily far future. The behavior is chaotic, because the effect of the initial perturbation leads to completely random outcomes as can be seen in Figure 2, where the trajectories of molecules are compared, which have experienced very slight differences in the perturbation. Quickly their direction of motion will be completely different.

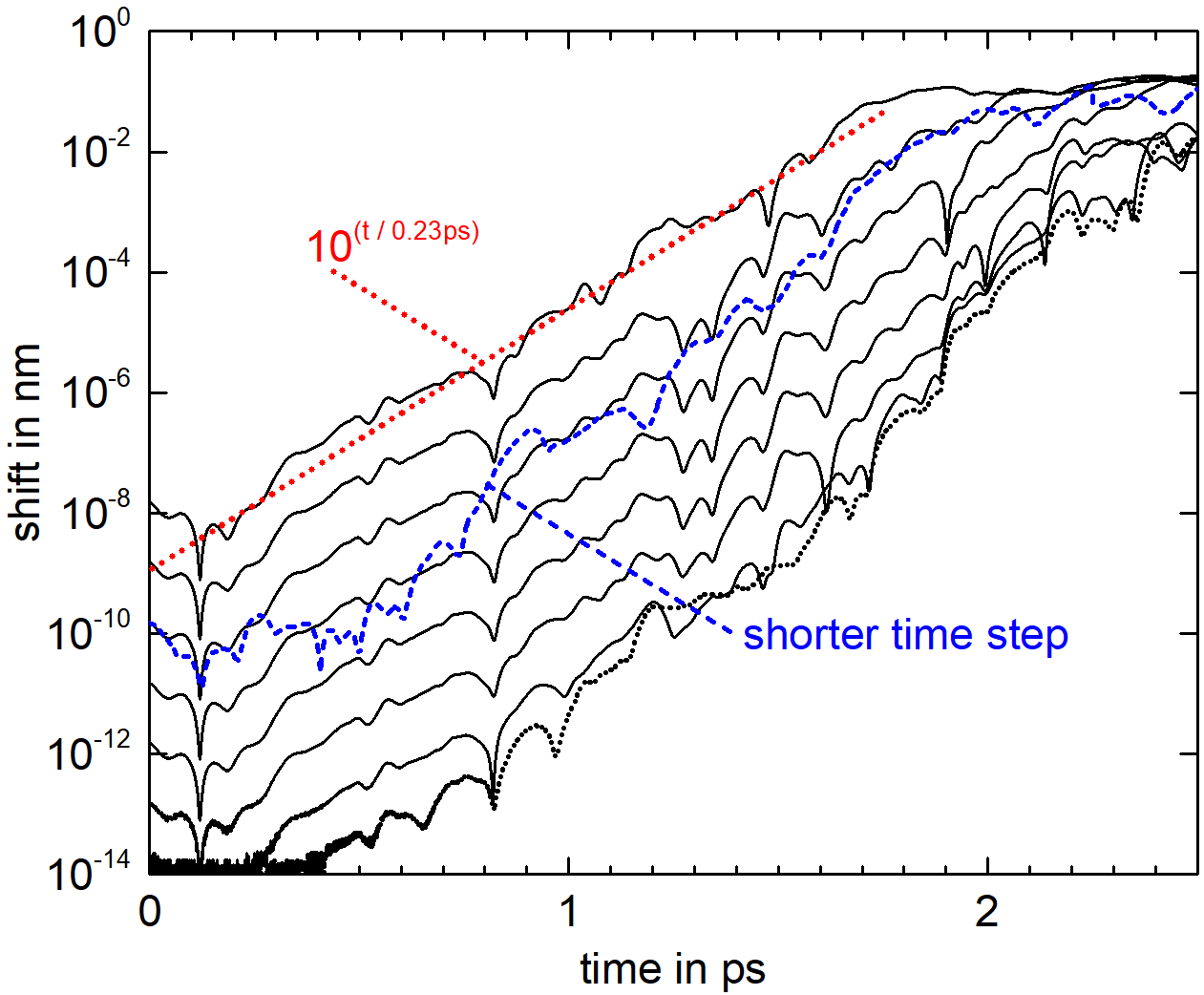
Figure 1: Deviation in position of a water molecule in liquid water at 37°C after initial perturbations of that water molecule of different size (reproduced after Pfennig, A. Eur. Phys. J. D (2018) 72: 45. https://doi.org/10.1140/epjd/e2017-80293-4)

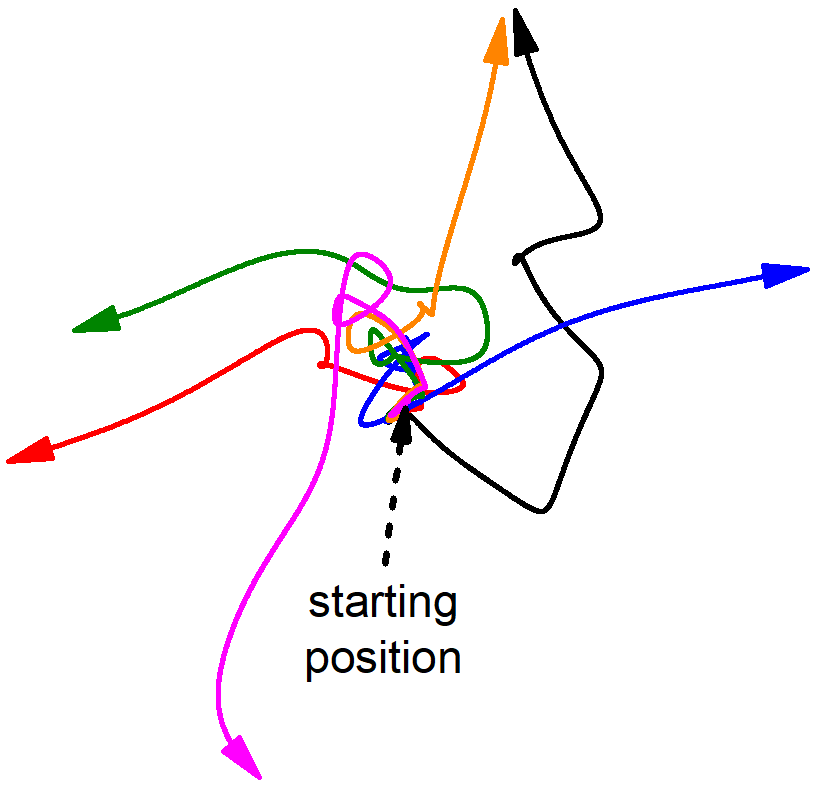
Figure 2: Randomization of molecular paths, if slightly different perturbations are introduced at the start position (reproduced after Pfennig, A. Eur. Phys. J. D (2018) 72: 45. https://doi.org/10.1140/epjd/e2017-80293-4)

If it is desired to predict the molecular behavior over some time, any inaccuracy in defining the starting conditions of the molecules with respect to their position and velocity would increase exponentially exactly at that speed indicated. Thus, the required accuracy in defining the starting positions and velocities would correspondingly quickly increase, if the time, over which the prediction is desired, would increase. For every 0.23ps farther into the future, the starting conditions would need to be specified by one more decimal digit. For a prediction over just 33ps - where it will become obvious only later, why specifically this time is chosen - the accuracy required would be almost 145 decimal digits. Of course also the computations would need to be performed with that accuracy. Of course this is only a practical infeasibility, in principle further increasing the accuracy would allow to extend the prediction time arbitrarily. Prediction nevertheless becomes practically infeasible already for relatively short prediction times. In chaos theory, this effect is typically expressed such that it is practically not possible to predict the molecular behavior beyond an intermediate timescale.

Another implication of this deterministic chaos becomes obvious, if the effect of a faraway influencing molecule is observed on a system of liquid molecules. For simplicity, only gravitational interactions are regarded, which avoids quantum effects. The farther the influencing molecule is away from the observed system of liquid water, the smaller the force of interaction will be. Nevertheless, this small interaction force will lead to a shift in position of the observed water molecule. This shift will in turn increase exponentially according to the deterministic chaos explained above. The question can then be asked, how long it takes, until an interaction with a influencing molecule will affect the observed molecule to a given degree, for example until a shift in the position of the observed molecule becomes obvious. Such a shift is obvious, if it is of the order of a molecular diameter, because then the shift corresponds to a so-called bifurcation. If a molecules for example decides, if it moves past a neighboring molecule to the left or the right, the difference of that position is of the order of a molecular diameter and the distinction in future molecular pathway corresponds to such a bifurcation. The molecule decides (forks) between the two option, which constitute the bifurcation. The time until that bifurcation occurs depends of course on the distance between the influencing and the observed molecule. This dependency is shown in Figure 3.

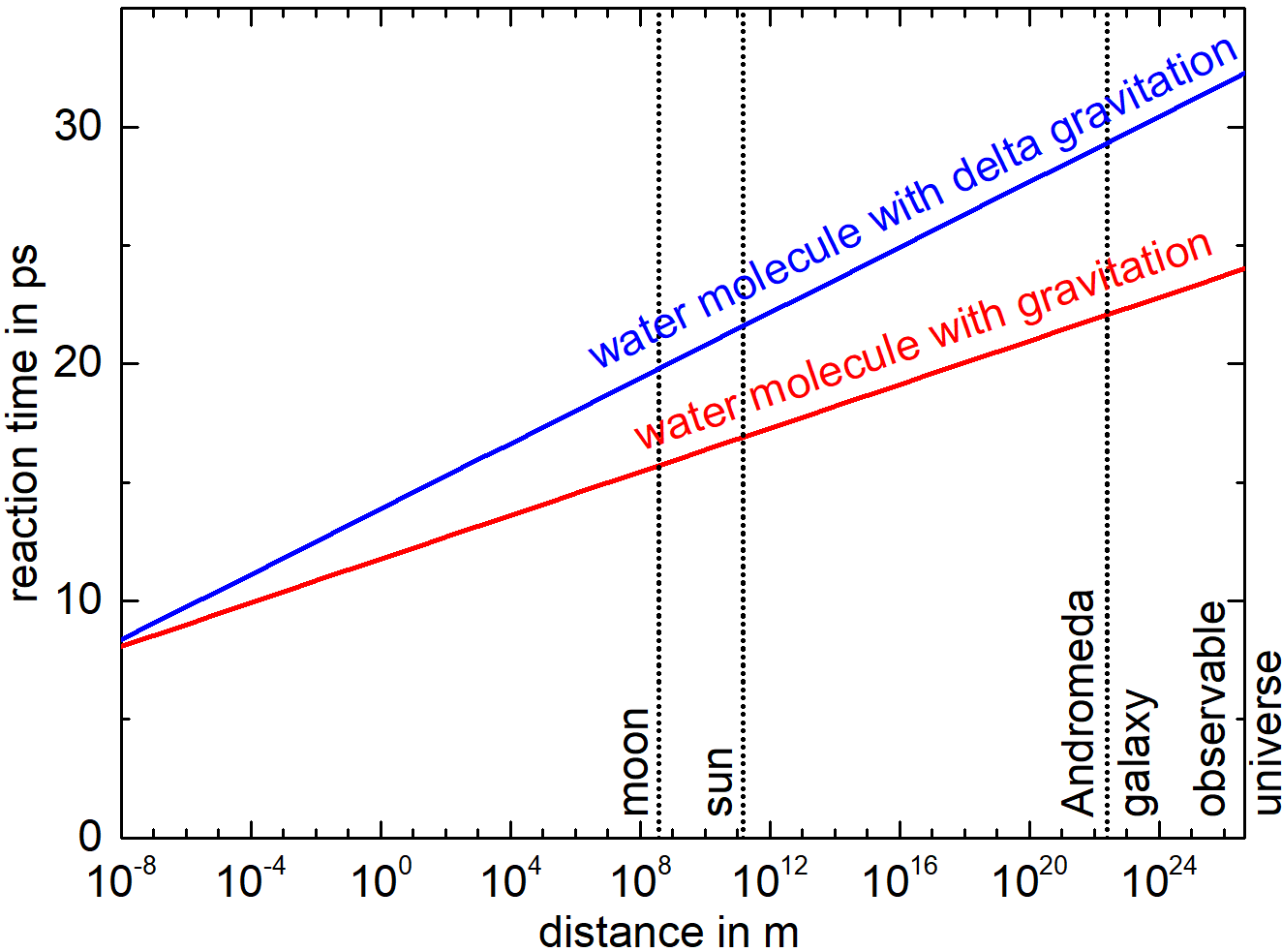
Figure 3: How long does it take, until an interaction between a faraway molecule with an observed water molecule in the glass of water on the table will lead to a shift by one molecular diameter, which corresponds to a bifurcation? (reproduced after Pfennig, A. Eur. Phys. J. D (2018) 72: 45. https://doi.org/10.1140/epjd/e2017-80293-4)

Actually, the interaction with neighboring water molecules in the observed system, which can be visualized as a glass of water on a table, will be quite similar, because their distance to the faraway molecule is almost identical. The deterministic chaos effectively will only be originating from the difference in force acting on the neighboring molecules. Accounting only for this force difference, the effect is shown in Figure 3 as well, indicated as 'delta gravitation'.

It is obvious that the farther away the interacting molecule is, the longer it takes, until the bifurcation occurs. It is interesting to observe though that the overall time required is small even for largest distances. Even, if the interaction occurs originating from a molecule at the end of the observable universe, it takes only 33ps! That is 33 times a millionth of a millionth of a second. Of course the travelling time of that interaction has to be accounted for. Thus, the interaction with a faraway molecule has to be considered that is momentarily arriving at the observed molecule in the glass of water, but which originated much earlier in time. Thus, interactions occur with molecules that existed corresponding times ago. For gravitation, it is today assumed that it travels at the speed of light. If a water molecule on the moon is considered as an example, where the light needs a little more than a second to reach us, the interactions of the molecules in the glass of water occur with the moon water molecule as it existed little more than a second ago. Once that interaction arrives at the glass of water, the reaction of that observed water leads to a bifurcation after only around 20ps. If, as an extreme case, a molecule at the end of the observable universe is regarded, which is defined as that horizon, which corresponds to the big bang, then the interaction has travelled since the big bang, but once it arrives at the glass of water, the molecular reaction takes only 33ps.

The interactions can thus be viewed as follows:

• All particles in the universe constantly send their information in all directions, which are relevant for their interactions with other molecules. This information travels at most with the speed of light.
• All particles in the universe receive that information and react to the overall force resulting.
• After at most 33ps any individual interaction will have influenced the observed particle to a degree that corresponds to a bifurcation. Influencing molecules, which are closer, will have a faster influence.

This also applies despite so many particles interacting, because the interactions of all particles are linearly superimposed. Thus, if a single particle at the end of the observable universe were not there or in a slightly different place, the behavior of an observed particle would be different by a molecular diameter 33ps after that interaction arrived at the observed particle. Thus, all particles experience a highly inter-connected network of interactions, where each individual particle is relevant, and where each particle quickly reacts to the extremely fine microstructure of forces acting. This describes the interactions as they exist and is not just a statement about practicability of prediction as typically expressed for chaos theory as described above.

The 33ps are here to be regarded as a maximum, because in the simulations on which this evaluation is based, rigid water molecules have been assumed. It is to be expected that the timescale will be significantly shorter by orders of magnitude, if degrees of freedom are included in the consideration, which have higher frequencies like the intra-molecular vibrations or motions of elementary particles within the molecule.

If the interactions between particles are accounted for, the question can again be regarded, what it means, if the behavior of a system shall be predicted over 33ps. In that case all interactions with all particles in the observable universe would need to be accounted for as they are locally arriving. That means that the most distant particles need to be accounted for at the positions they had at times of the big bang. This is of course much more demanding than to perform the simulation with 145 significant digits as resulted from chaos theory as described above. Thus the interactions among particles render any prediction fundamentally impossible even for very short times. Also this statement is thus much stronger than what is typically stated in the context of chaos theory.

Deterministic chaos does not only occur on molecular level. Any system, which is sufficiently complex and especially includes feedback loops of interactions, will show Lyapunov instability. On molecular level, the feedback results from molecules interacting with molecules, with which they collided or interacted just a short moment before, which thus react to each other. Thus, it can be expected that the effects described here also apply to a variety of other systems on various scales, if they show sufficient complexity and especially similar feedback loops.

As a note it should be added that this also has significant implications for the arrow of time. In physics it appears that in almost all physical laws the direction of time could be inverted and the system could then identically run in backward. The question is then posed, why time runs in forward direction and not in backward, thus, why reality has chosen to run forward. Popper already realized that in a time reversal all waves would need to run backward very accurately in order to finally contract to a single point which coincides with the event initiating the waves (Popper, Karl R. 1956. The Arrow of Time. Nature 177, 538). From the considerations here, the statement can be much intensified. If it were intended to inverse time at some point, observing the inverted system for only 33ps would require that all particles everywhere in the observable universe would need to be accounted for since the big bang, and all their interactions would need to be running very accurately backward so that the influences contract to the positions of the particles, from which they originated in forward direction. This invertibility until be big bang for reversing time only by 33ps is of course again a much stronger statment.

This shows that while the physical laws may be insensitive to the inversion of time, the initial conditions are not. In forward time, one would be free to arbitrarily define the initial conditions. In backward time, the initial conditions would need to be chosen such that the entire network of interactions is properly inverting, which is fundamentally impossible. Inversion would thus only be possible starting out from a system that has previously developed in forward direction, which renders backward direction of time not the primary direction. It should be stated clearly, that these consideration only refer to the physical laws and not neccessarily to the reality itself. As already Ernst Mach stated: "Nature simply is." (Ernst Mach: The Science of Mechanics. A Critical and Historical Account of its Development. Translated by Thomas J. McCormack. The Open Court Publishing Co., Chicago, 1919) Nature thus does not care about the peculiarities of our physical description.

Finally, it has to be clear that the picture described here assumes a fully deterministic world view. This means that with the exact physical laws, a given starting situation will lead to an unavoidable and unique future development, which is solely defined by the physical laws and the initial conditions. Thus, either reality behaves as described or the physical deterministic laws are not properly describing reality. Of course on quantum level typically non-deterministic behavior is assumed. Unfortunately it has been shown that also quantum systems undergo Lyapunov instabilities. Thus, also the consequences apply to the quantum world. The question finally is, if the stochastics usually assumed for the quantum world are not actually induced by the effects described here, while the actual quantum elements behave deterministically, which due to the smallness of the quantum elements can only not be observed experimentally.